 国家高新企业 | ISO9001认证
国家高新企业 | ISO9001认证 二级病原微生物安全实验室
二级病原微生物安全实验室- 联系电话:+13336028502
- +400-161-1580
- service@guheinfo.com


谷禾健康


在现代测序技术的帮助下,微生物组研究的范围被扩大,通过16S rRNA测序或鸟枪法宏基因组测序可以生成大量的微生物组数据。而微生物群落研究中的一个重要问题是对这些微生物的归类,模拟和分析人类微生物群。
通常使用16S rRNA技术量化微生物群落的组成,但量化后的数据是偏斜的,带有过多的0。目前还缺乏对复杂的微生物群落测序数据的标准化的聚类分析方法。
近日,加拿大多伦多大学研究人员在《Microorganisms》上发表的一篇研究,针对上述问题构建了一个参数化的混合模型用于计算聚类分析的距离度量,模型根据观察到的OTU计数和估计的混合权重产生sample-specific的分布。这个方法可以准确的估计真实的0比例,从而构建一个精确的beta多样性度量。
大量的模拟研究表明,与一些被广泛使用的距离度量方法相比,当存在较大比例的0时,该方法取得了较好的聚类效果。
该研究人员提出了一种具有特定beta多样性度量的聚类算法,该算法可以解决稀疏计数数据遇到的有无偏差问题且能有效的度量样本距离,达到分层的目的。
微生物群落研究中的一个重要问题是对这些微生物的归类,它们是否能被划分为亚群。如果有,有多少组亚群,如何解释这个亚群。例如,这种分类是否区分了治疗方法、疾病或遗传类型。
为了回答这些问题,需要测量两个微生物群落之间的相似性。beta多样性是为了适应不同的目的而提出的,在评估群落之间的差异时提供不同的结果。对于微生物组成,beta多样性根据测量丰度来衡量群落之间的距离,丰度可以是观察到的计数,也可以是相对丰度,这些丰度是根据不同或距离度量计算出来的,以量化样本之间的相似性。
现如今,已经有许多非参数统计方法来量化距离度量。例如Euclidean和Manhattan距离是最常用的。其它beta多样性指标,例如Bray-Curtis距离、Jensen-Shannon距离、Jaccard指数、UniFrac距离(未加权的、加权的和广义的)也经常用于微生物组研究。
除了距离度量之外,还引入了用于生态关联推理的稀疏逆协方差估计(SPICE-EASI)的图形网络模型。然而这些方法都会有一定的局限性,例如SPIEC-EASI方法依赖于单一的方差-协方差矩阵,由于微生物群落结构复杂,可能无法完全恢复底层OTU网络。
于是,研究人员开发了一种创新的聚类方法,以混合模型而不是beta多样性度量作为距离度量,并将聚类算法应用于微生物群落数据来表征亚群。该算法还包括根据选择的内部指标选择最优聚类数,并将结果在几种距离度量和不同评估方法之间进行比较。通过全面的模拟研究和一个真实的帕金森病肠道微生物群数据集对该算法的性能进行了评估。
1. 构建混合模型
混合模型是一种概率模型,用于表示在无监督学习中经常使用的总体内的子群体。该模型关注单个OTU在种群中的分布,可以解决样本间的稀疏性问题。它参数化地模拟了计数的潜在分布,包括低计数OTU和极高计数。对于个体样本之间的成对距离,在L2范数距离中使用公式化的混合概率。
2. 距离度量
在确定混合模型分布后,使用概率分布通过样本之间的两两距离计算距离度量。为了进行比较,考虑了基于L2范数的三种距离度量(L2-PDF、L2CDF、L2-DCDF、L2-CCDF)。
除此之外还选择了一些其他的距离度量进行比较,即Manhattan距离和Euclidean距离,以及微生物组分析中特有的三个距离度量:Bray-Curtis距离、加权UniFrac距离和广义UniFrac距离。本研究不考虑未加权的UniFrac距离,因为它不包含类群丰度信息。
3. 聚类分析验证指数
这些指数用于衡量集群在集群内部和集群之间的可分离性表现很好。验证指标可以分为内部指标和外部评估,许多内部验证指标被用来选择最优聚类数。外部评估分数是在假设标签在建模阶段没有使用时,通过直接将划分结果与之前的标签进行比较来计算的。
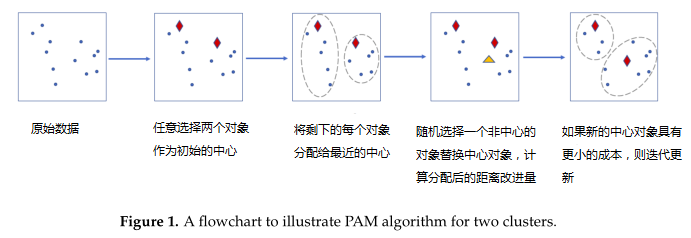
4. 用于聚类的分区算法(PAM)

使用混合分布的聚类过程的详细步骤:
为了测试该方法在聚类中的表现如何,研究人员推导了其准确性和Jaccard指数。
准确性是指聚类结果与真实的聚类指数的接近程度。它被定义为正确聚集的受试者所占的比例。
Jaccard指数衡量聚类结果与原始聚类标签之间的相似性,原始聚类标签定义为正确分类的主题数量(预测集与真实集的交集 )与两组总样本量(两集的并集)之比。
研究人员用类标签模拟数据来模拟OTU计数及其复杂的结构。研究人员考虑两个有两个子类和三个子类的场景,每个子类包含200个样本,总样本量分别为400和600。所有的结果被重复了100次。
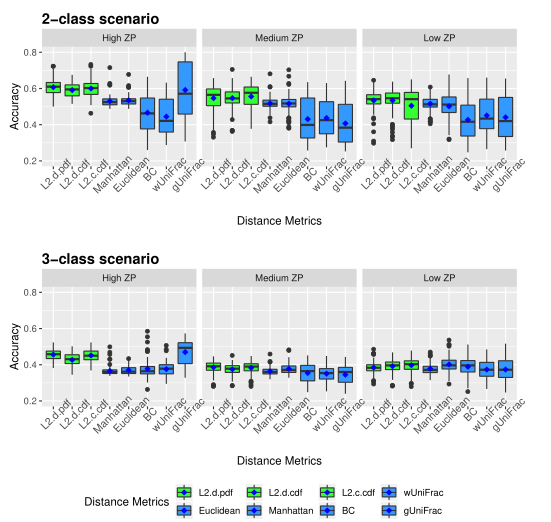
下图展示了模拟数据的准确性。评估了三种不同的0的比例(ZP)情况,左中右分别为高ZP、中等ZP、低ZP。
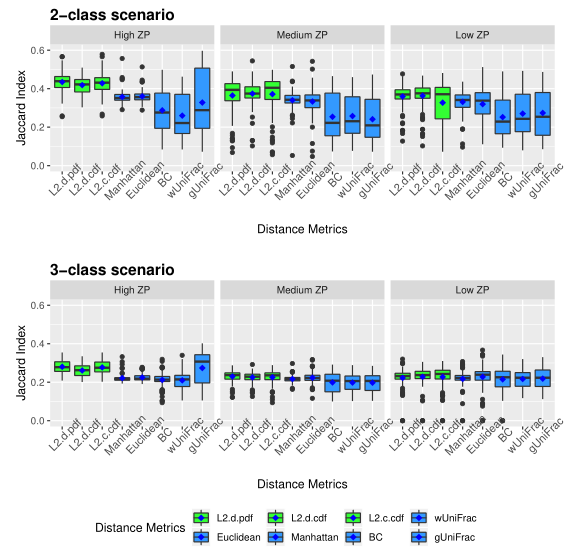
下图展示了模拟数据的Jaccard指数。同上图一样评估了三种不同的0的比例。
以上两图显示了具有不同ZP和子类数量的不同场景下模拟数据集的聚类结果。通过准确率和Jaccard指数对基于距离的算法性能进行了评估。填充颜色为绿色的箱形图为研究人员建议使用的距离度量。所有的距离都是根据相对丰度计算的。
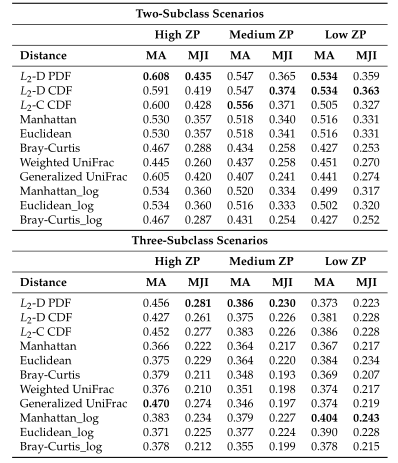
Table1平均准确率(MA)和平均Jaccard指数(MJI)估计。粗体表示每个方案下的最佳情况。Log表示对输入的模拟数据进行了对数变换。
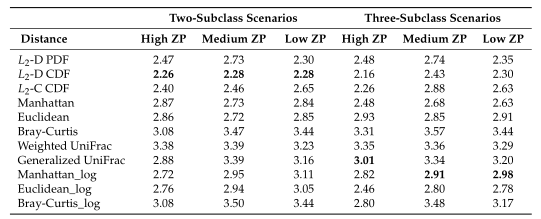
Table2所有模拟场景的平均集群数。根据Dunn内部指数计算出每次重复的最优聚类数。
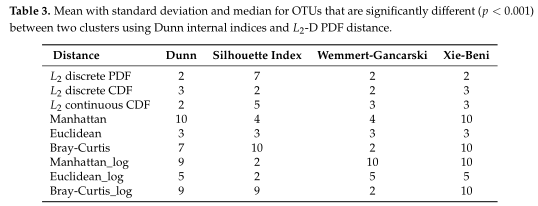
Table1 的结果是通过对每个场景中的100个重复结果求平均值计算得出的。观察得到在聚类算法中实现的距离度量(即绿色标识的箱形图)的准确率和Jaccard指数都优于其他距离度量,特别是在数据集中包含大量0时(高ZP)。在MA和MJI方面,L2范数也显示了其优势,在基于100次重复计算的L2范数在两个子类场景下的;平均准确率约为0.6秒,在三个子类场景下的平均准确率为0.45。而广义Unifrac距离(gUniFrac)在准确性估计中有很大的波动变化。
数据集为197名PD患者和130名对照的粪便样本的16S rRNA测序数据。首先过滤掉在80%的OTU中相对丰度都为0的OTU,因此,此次分析中共使用280个OTUs。将基于相对丰度计算的L2范数与其他三个距离度量进行了比较,包括对数变换和不变换的比较。
如Table3所示,距离度量采用各种内部验证指标(列名)进行灵敏度分析。对于Dunn和Xie-Beni指数,l2范数倾向于将数据聚类为两到三个亚群,而在有和没有对数变换的情况下,除了未变换的欧氏距离外,Manhattan、Euclidean和Bray-Curtis更倾向于聚类更多的亚群。(设置了最多聚类数目为10)
接着选择L2-D PDF范数作为进一步分析的例子。
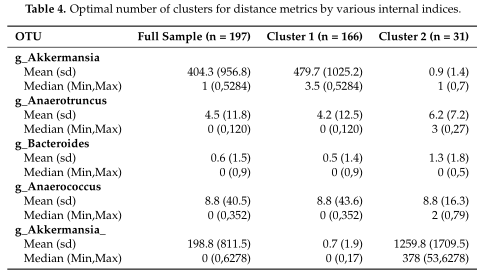
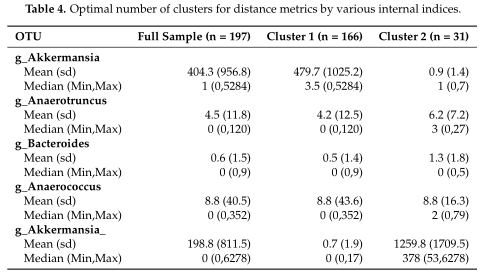
结果在Table4中展示,对数据集中的两个集群之间的OTUs进行了探索,得到了聚类之间差异最大的前5个OTU。
研究认为该聚类算法在高ZP和中等ZP的情况下表现最好,因此,当数据中出现大量的0时,建议使用。并且,在PAM框架下,文章中列出的那些距离度量都可以用作聚类的输入。
如模拟研究中显示的那样,在各种场景下,由混合模型计算的成对距离比其他距离度量表现的更好。但是与所有聚类方法一样,都有一个局限性,就是很难为每个新数据选择合适的内部指标,因此很难获得最优和最稳健的集群数。
此外,对于L2范数距离,在聚类中无法进行变量选择。但不可否认,该聚类算法结合了微生物测序数据的特殊距离,所介绍的聚类算法除了目前使用的方法之外,还可以被看作是分析微生物数据的一个很好的辅助工具。
研究人员指出,下一步会基于Dirichlet-Polyomial等模型进行分区,与文章中的方法进行比较,并努力将该方法扩展到其他微生物群落和疾病相关的数据上。
【参考文献】
Yang D, Xu W. Clustering on Human Microbiome Sequencing Data: A Distance-Based Unsupervised Learning Model. Microorganisms. 2020 Oct 20;8(10):E1612.